Kerbal Space Program es un juego / simulador de vuelo espacial que se ha hecho legendario en Internet. Han habido pocos juegos que hayan incluído vuelo espacial realista, porque el vuelo espacial es muy complejo como para ser divertido (aparte de unos cuantos pillados entre los que me incluyo), y porque el vuelo espacial real es muy diferente de como estamos acostumbrados a verlo en las películas.
El mérito de Kerbal Space Program es que incluye un modelo físico realista aunque simplificado (incluyendo gravedad y efectos atmosféricos), de forma que es relativamente accesible, pero suficientemente riguroso como para que uno acabe aprendiendo astrodinámica real.
Advierto: jugar a menudo al KSP arruina la experiencia de ver películas de ciencia ficción. Por otro lado, hace mucho más fácil seguir eventos científicos como el vuelo de la sonda Rosetta, New Horizons o Juno.
Trasteando con KSP uno aprende cosas como diseñar un cohete multietapa para entra en órbita, hacer citas orbitales, atracar, enviar sondas a la luna o planear una expedición interplanetaria. Que es lo que nos ocupa.
Parte de la accesibilidad de KSP es que uno diseña cohetes a base de ensamblar piezas estándar (un poco como jugar con lego) para luego poner una capsula tripulada en órbita... o provocar enormes explosiones. Lo que hace KSP a la vez entrañable y poco serio es que uno no trabaja con astronautas humanos, sino con "Kerbals", una especie de humanoides verdes con un profundo amor por la ingeniería y a su vez poco respeto por su propia integridad física.
(Enviar una expedición tripulada de ida y vuelta a Eve es uno de los desafíos más grandes que uno pueda plantearse en KSP).
Tras Ceres viene Jool, el equivalente de Júpiter, y al igual que en nuestro sistema solar, el planeta más interesante, con cinco satélites: Laythe, Vall, Tylo, Bop y Pol. Laythe es especialmente interesante, porque es un satélite oceanico con varios archipiélagos dispersos en su superficie, y una atmósfera no respirable pero similar a la de Kerbin, de forma que el cielo es azul y ofrece tremendas vistas de Jool, dado que es el satélite más cercano.
La navegación espacial real no es en absoluto intuitiva, y las naves espaciales reales tienen multitud de instrumentos (y apoyo desde la Tierra) para saber en todo momento dónde están, en qué dirección se mueven, y cómo realizar maniobras.
Una pequeña aclaración: cuando estoy hablando de DeltaV para ir de una órbita a otra, estoy mencionando sólo la magnitud del cambio de velocidad, y no la dirección. A efectos de calcular el presupuesto energético del que dispongo, es suficiente con hablar de DeltaV como una magnitud escalar. La orientación del vehículo cuando cambie de una órbita a otra no es relevante para esta discusión, pero la mencionaré si es necesario.
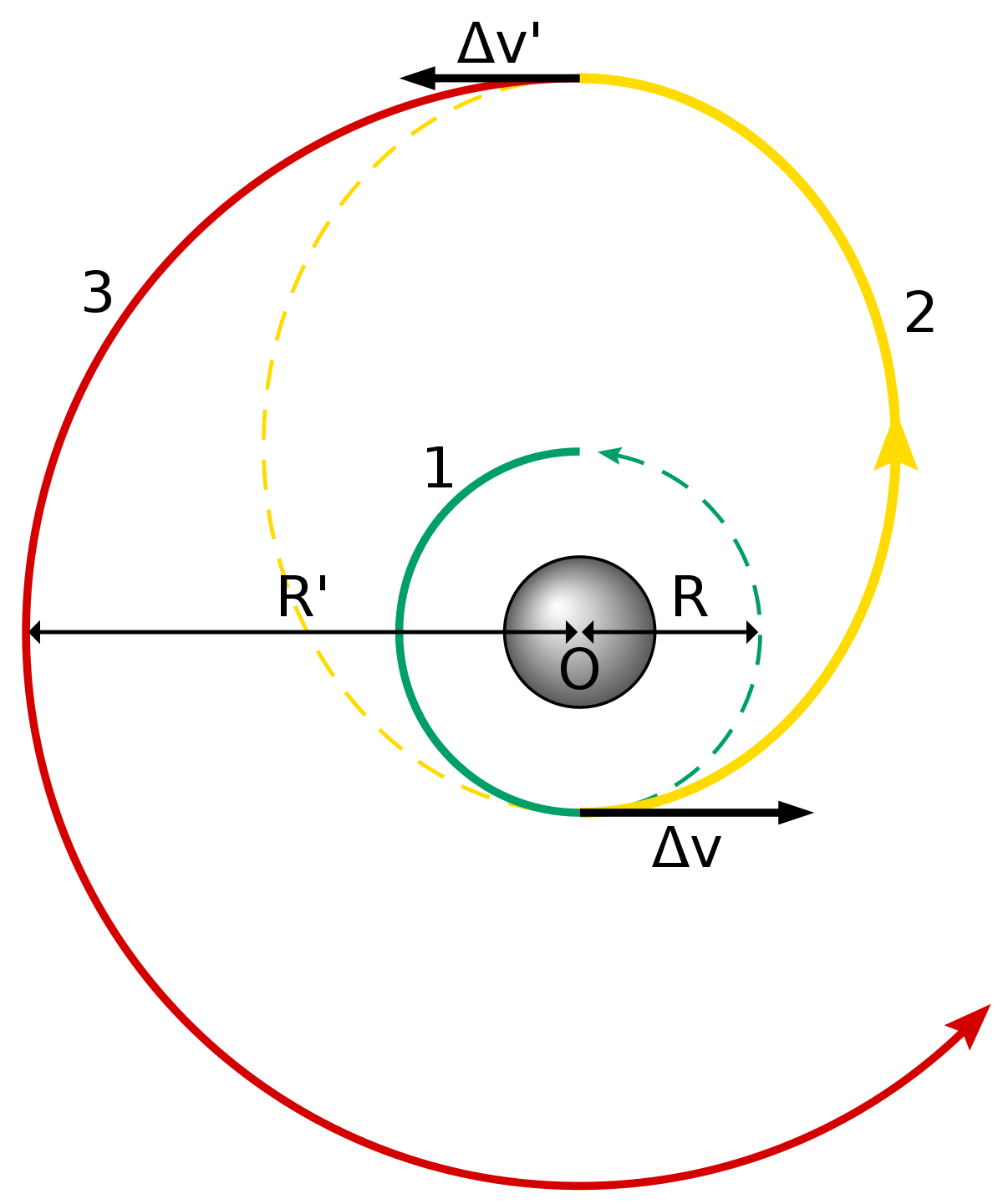
En esta formulación de la ecuación del cohete, tenemos Vexh, que es la velocidad a la que se expulsa el propelente, la fracción de masas m0/m1, que es la relación entre la masa total del vehículo y la masa "seca" del vehículo (o sea, sin propelente).
Hay que tener en cuenta que la eficiencia de un motor cohete depende de la presión ambiental, y por ello, el Isp varía según estemos al nivel del mar o en el vacío. El Isp en el vacío es mayor que al nivel del mar.
- La primera etapa nos da la DeltaV para despegar y poner el cohete en órbita.
- La segunda etapa nos da la DeltaV para ir a Mun, entrar en órbita, y si queda algo de margen, ejecutar parte o toda la maniobra de aterrizaje.
- El módulo tripulado nos da la DeltaV para aterrizar en Mun, volver a despegar y salir de la órbita de Mun, de forma que la trayectoria entre en la atmósfera de Kerbin.
- La cabina del módulo tripulado la separamos del resto, y le ponemos un escudo térmico y paracaidas, de forma que una vez la trayectoria orbital entre en la atmósfera, el rozamiento nos frene y podamos hacer un aterrizaje suave, sin necesitar más propelente.
Para planificar las misiones, los usuarios de KSP han hecho mapas de DeltaV, parecidos a los mapas del metro, que listan la DeltaV para ir a diferentes partes del sistema kerbolar, partiendo de Kerbin:
Para hacer este mapa se han asumido varias cosas. Principalmente, se supone que para ir de un cuerpo a otro, uno utiliza la trayectoria óptima en términos de consumo de fuel, esto es, una órbita de transferencia de Hohmann. De las órbitas de transferencia de Hohmann hablaré más abajo.Esto no tiene que ser siempre el caso, pero lo único que hay que tener en cuenta es que, si no uso una transferencia de Hohmann, voy a necesitar más DeltaV. Este mapa, pues, me da el gasto mínimo de DeltaV que necesito para ir de un sitio a otro, y generalmente tendré que planear mi vehículo con algo de margen.
Por ejemplo, supongamos que quiero ir de Kerbin a Mun. Necesitaré 3400m/s para despegar y entrar en una órbita baja, 860m/s para entrar en una órbita de transferencia a Mun, 360m/s para entrar en órbita en Mun, y 580m/s para aterrizar. O sea, que mi cohete deberá tener al menos 5200m/s de DeltaV en el momento del lanzamiento. Si además quiero volver, tendré que dieseñar mi vehículo con aún más DeltaV.
Para poner una sonda en la superficie de Duna, necesito un cohete con unos 6540m/s de DeltaV. Para una carga de pago pequeña, esto no es un cohete necesariamente muy grande. Si quiero llevar una nave tripulada, y quiero volver, necesito otros 3140m/s de DeltaV.
Si quiero llevar una cabina de mando y un módulo de habitáculo, el cohete empieza a ser gigantesco, así es que puede ser ventajoso montar el vehículo en órbita (requiriendo varios lanzamientos). Además, en estos casos conviene separar el vehículo de transferencia (que incluirá los motores, tanques de propelente y el habitáculo de la tripulación),del módulo de aterrizaje, de forma que para aterrizar no necesitamos tanto propelente (porque no aterriza toda la nave), y a la vuelta desechamos el módulo de aterrizaje, de forma que ahorramos propelente no teniendo que cargar con él.
(Esto es lo que hicieron las misiones Apollo).
Quiero terminar este largo post hablando de cómo se planea un viaje entre planetas. Si quiero usar una órbita de transferencia de Hohmann, tengo que esperar a que los planetas estén alineados para que, empezando el viaje en un momento determinado, el planeta de destino esté en el punto de su órbita en el que intercepta a mi órbita de transferencia.
Volvamos a las órbitas de Hohmann. Una transferencia de Hohmann es una órbita elíptica que se utiliza para pasar de una órbita a otra alrededor de un cuerpo central (vamos a asumir que tanto la órbita de origen como la de destino son circulares). La órbita de transferencia tiene la periapsis en la órbita más baja, y la apoapsis en la órbita más alta. Supongamos que queremos pasar de la órbita más baja a la órbita más alta. Para entrar en la órbita de transferencia, efectuaríamos un encendido en la dirección del movimiento (lo cual se llama progrado) cuando nuestra órbita y la de transferencia se tocan. Posteriormente, una vez lleguemos al punto donde la órbita de transferencia y la órbita superior se tocan, volveríamos a efectuar un encendido en la dirección del movimiento para circularizar nuestra órbita.
Para pasar de una órbita más alta a una más baja, el procedimiento es el mismo, realizando los encendidos contra la dirección del movimiento (retrógrado).
By Leafnode - Own work based on image by Hubert Bartkowiak, CC BY-SA 2.5, Link
Para este tipo de maniobra se asume que los encendidos suceden idealmente en un tiempo infinitesimalmente pequeño. En un motor real tenemos que encender el motor durante un tiempo determinado (no nulo) para efectuar el cambio de velocidad que necesitamos, perdiendo un poco de eficiencia.
El problema lo podemos plantear así: si uso una órbita de transferencia con un tiempo de vuelo conocido, quiero saber en qué punto de la órbita del planeta de origen tengo que iniciar el viaje para encontrarme el planeta de destino en el punto en el que mi órbita de transferencia y la del planeta de destino se encuientran.
El ángulo entre los vectores de los planetas de origen y destino al iniciar el viaje se llama phasing angle (ángulo de fase). En esta página está explicado como calcularlo, pero los usuarios de KSP son muy listos y han creado un applet para calcularlo automáticamente sin tener que ocuparse de las matemáticas.
Este punto de la órbita en el que tenemos que iniciar el viaje para poder usar una órbita de transferencia de Hohmann es lo que se denomina transfer window (ventana de transferencia). Como queremos ahorrar energía (o sea, utilizar la menor DeltaV posible), no podemos enviar misiones a Marte (o en KSP, a Duna) cuando nos de la gana, sino cuando los planetas estén alineados adecuadamente.
Hay una forma todavía más sofisticada de encontrar el momento correcto para iniciar una transferencia interplanetaria. Es lo que se denomina porkchop plot, o algo así como "diagrama de costillas de cerdo". Este es el método que utiliza la NASA para planificar sus misiones.
Lo que es el porkchop plot está explicado aquí o aquí. El porkchop plot es una representación gráfica de las soluciones del problema de Lambert. El problema de Lambert consiste en encontrar una órbita que pase por dos puntos en el espacio y tenga un tiempo de tránsito determinado. Este problema se puede resolver analíticamente, o utilizando métodos iterativos. Representando gráficamente las soluciones del problema de Lambert obtenemos el porkchop plot: en este diagrama, los ejes representan el tiempo de partida y el tiempo de llegada para una transferencia entre dos cuerpos celestes, y la tercera coordenada es la energía característica de la órbita que resuelve el problema. Las curvas de nivel, pues, son curvas que unen las soluciones de igual energía. Para encontrar la órbita de menor consumo de energía (menor DeltaV), buscaremos los valles del porkchop plot.
El porkchop plot puede representarse con curvas de nivel, como en el artículo de Wikipedia, pero también se puede representar con colores, como han hecho aquí. Sin siquiera entender las matemáticas, puedo introducir el planeta de origen y el de destino, y en el porkchop plot tengo representada la DeltaV que necesito para una fecha de salida y un tiempo de tránsito determinados. La DeltaV está representada en colores, y el azul oscuro representa el mínimo de DeltaV. Así es que pulsando en el diagrama en un punto determinado, dependiendo de cuánta DeltaV quiera consumir, los ejes me dicen cuándo tengo que iniciar el viaje interplanetario y cuánto durará el viaje.
En una misión real tripulada, el tiempo de viaje es vital a la hora de saber qué cantidad de suministros necesito para tener a la tripulación viva y en condiciones de trabajar. El consumo de alimentos y oxígeno no está incluído en el KSP básico... pero hay mods que lo añaden, para aumentar el realismo y tener un desafío más al que enfrentarse.
Hasta aquí llega la teoría de la planificación de misiones interplanetarias. En el próximo post explicaré qué preparativos he hecho para enviar kerbals a Duna.





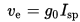




Después de leer el post me han entrado unas ganas casi irresistibles de comprar KSP para la PS4 :-) Pero va a tener que esperar un poco, hasta que la vuelva a desempaquetar.
ResponderEliminarLa entrada da gusto leerla (y además no conocía los porkchop plots, así que encima he aprendido algo).
Una pregunta me ha quedado sin responder: ¿cómo afecta a la órbita de Hohmann que origen/destino no sean coplanares? ¿es ése el caso en el sistema solar de los Kerbals?
Un saludo y muchas gracias por componer de nuevo,
En primer Lugar, KSP ya no está para la PS4. Take2 compró el juego y lo retiró de la tienda de PSN. De todas formas, el juego no llegó a estar disponible en Europa debido a problemas con la certificación.
EliminarPara más inri, el port de KSP a la PS4 tenía un montón de bug, y además, como juego de consola no tenía soporte para mods, así es que muchas de las cosas que comento en el post iban a ser mucho más complicadas de hacer.
En cuanto a la segunda pregunta, el problema de que las órbitas de los planetas no estén en el mismo plano lo iba a comentar en el siguiente post, pero puedo explicarlo "brevemente".
Efectivamente, si las órbitas de los planetas no están en el mismo plano hay que añadir una componente normal / antinormal al encendido para entrar en la órbita de transferencia.
La forma de cambiar de plano entre dos órbitas es hacer un encendido en la dirección normal o antinormal de la órbita en el nodo de las dos órbitas (un nodo es el punto en el que dos órbitas con diferentes planos se cruzan). La dirección normal es la dirección perpendicular a la órbita, según la norma de la mano derecha. O sea, en una órbita ecuatorial en dirección hacia el este, como es habitual, la dirección normal sería hacia el norte (y la antinormal sería en el sentido contrario, hacia el sur).
Como ya digo, el cambio de plano se hace con un encendido en el nodo de la órbita. Ahora bien, cuando tengo una ventana de transferencia, el planeta de origen no está necesariamente en el nodo de la órbita. Así es que en ese caso haría la transferencia de forma normal, entrando en una órbita solar, y haría el encendido de cambio de plano cuando llegara al nodo de la órbita de transferencia, esto es, el punto en el que la órbita de transferencia y la órbita del planeta de destino se cortan.
En el caso de KSP, los planetas no orbitan todos en el mismo plano alrededor del sol, pero las inclinaciones varían. Entre Duna y Kerbin no hay mucha diferencia, y la inclinación se puede despreciar. Moho tiene una órbita fuertemente inclinada, y es bastante engorroso enviar misiones allí. Yo mismo envié una sonda de aterrizaje a Moho y no tuve en cuenta el cambio de plano, de forma que al tener que corregir la trayectoria me quedé corto de DeltaV como para aterrizar. Esto lo solucioné cambiando el nombre de la sonda de "Moho Lander" a "Moho Impactor". Ooops…
En el mapa de DeltaV del sistema kerbolar que está incluído en el post está indicado el coste del cambio de plano: en cada ramal que contiene la DeltaV de la transferencia hay un número encima que indica la DeltaV para ese el cambio de plano. En el caso de Duna son 10m/s y para Eve son 430 m/s. En el caso de Moho tenemos 2520 m/s, que es el triple de lo que cuesta la transferencia en sí.
Dicho esto, al final lo que hace uno es trastear con el interface para crear maniobras, hasta que la trayectoria predicha por KSP al llegar al planeta de destino es adecuada para la misión. Cómo se hace esto intentaré explicarlo en el próximo post.