Vámonos a Duna, parte II: De las fórmulas al tablero de diseño

Antes de continuar, me gustaría aclarar una cosa. En el pasado post estuve todo el tiempo hablando de propelente, que es el material que expulsamos de un cohete para producir movimiento en la dirección contraria. Cómo expulsamos el propelente, y cómo lo aceleramos para que nos de el mayor empuje posible es una cuestión distinta.


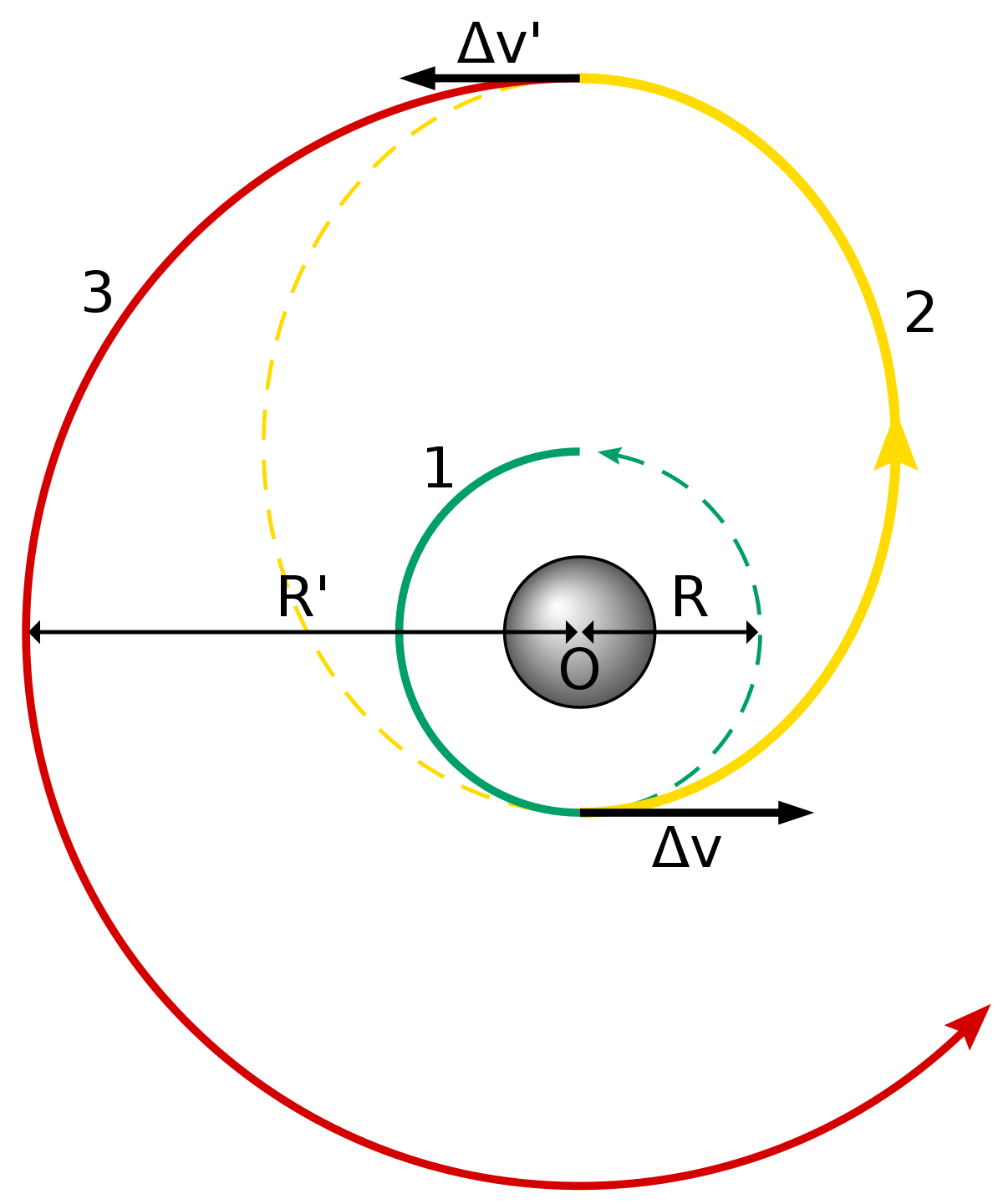
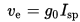En cohetes químicos, la forma de producir empuje es teniendo dos compuestos químicos: un oxidante y un combustible, que ponen en contacto provocando una reacción de oxidación-reducción, y produciendo calor y gases que se expanden rapidamente, impulsando al vehículo en la dirección opuesta. En este caso, tanto el oxidante como el combustible son propelentes, y hablaríamos de un sistema bi-propelente.


Otra forma de producir empuje es calentar un fluído en un reactor nuclear y expulsarlo a gran velocidad. Este es el principio de los motores nucleares térmicos. Este tipo de motor fue desarrollado por la NASA en varios proyectos, y se llegaron a construir y probar prototipos. Los proyectos acabaron siendo cancelados, dado que la única aplicación para la cual la mayor eficiencia de los motores nucleares era necesaria eran las misiones tripuladas de larga duración (como viajes a Marte o más allá), y a partir de los años 70 se decidió limitar las misiones tripuladas a la órbita terrestre.

En el KSP no hay diferentes tipos de propelente: el oxidante es siempre oxígeno líquido y el combustible es siempre hidrógeno líquido. Los aviones utilizan solamente combustible (el oxidante es el oxígeno de la atmósfera, como en una avión real), y las piezas de los aviones (como los tanques) se pueden utilizar en cohetes y viceversa. Así es que se da la situación de que los aviones consumen hidrógeno líquido en lugar de keroseno, como tendría que ser, pero esto es una pequeñez que no afecta al juego.

(Naturalmente, hay mods que añaden propelentes realistas).

He explicado esto porque es importante para algo que voy a contar más abajo. Vamos a ver pues unas cuantas soluciones prácticas al problema de enviar Kerbals a Duna.


Después de enviar misiones a Mun y Minmus con cápsulas diseñadas para este propósito, y a veces con vehículos similares a Apollo (o sea, un módulo de mando y servicio, y otro de aterrizaje), decidí que quería crear un sistema más genérico que fuera modular y que se pudiera adaptar a diferentes misiones. En este sistema tendríamos:

• Un módulo de propulsión, que contendría los motores y tanques de propelente
• Un módulo de habitáculo, para alojar a la tripulación
• Un módulo de mando, que permita pilotar el vehículo
• Uno o más módulos de aterrizaje, ya sea tripulado o automático, si queremos visitar un cuerpo celeste.
• Tanques adicionales, según necesitemos más o menos DeltaV para realizar una misión.

Hay una limitación al montar naves en órbita, y es que los módulos hay que ensamblarlos usando puertos de atraque. El problema es que los puertos de atraque son flexibles y hacen que las naves construídas con módulos grandes se comporten como macarrones mojados si se intenta hacerlas girar con demasiado ímpetu. En casos extremos, es posible que al hacer girar una nave se produzca una oscilación resonante y la nave se desmoche sola.

Este fenómeno se produce porque KSP simula físicamente las partes de cada vehículo. Esto añade realismo... pero a veces, a uno le gustaría que las naves de comportaran como un sólo cuerpo rígido.
Sobra decir que hay mods para crear junturas rígidas entre módulos, e incluso para añadir cuerdas para sujetar objetos y mangueras para transferir recursos entre módulos.

Así es que uno sólo puede tomarse libertades hasta cierto punto, y es conveniente seguir unos cuantos principios básicos:

• Construir las naves tan compactas como sea posible
• Asegurarse de que el vector del empuje de los motores pase por el centro de masas de la nave (porque, de lo contrario, la nave tenderá a girar cuando se enciendan los motores)
• Construir naves simétricas (porque si hay una asimetría en la distribución de la masa, igual que en el punto anterior, la nave tenderá a girar cuando se enciendan los motores)
• Como corolario del punto anterior, incluso aunque la nave sea simétrica, hay que asegurarse de que el propelente está distribuido por igual en todos los tanques, o la nave tenderá a girar al aplicar un empuje.

Pues acto seguido paso a mostrar mis ideas para enviar Kerbals más allá de la órbita de Kerbin.

Mi primera idea fue esta nave con el ocurrente nombre de Orbital Ferry MkIV Advanced:

 

(Para mayor claridad, he quitado todo el resto del cohete que pone a este módulo en órbita).

La nave que muestro es únicamente la sección de propulsión. Hay puertos de atraque delante y detrás para añadir módulos adicionales.

Para aumentar la cantidad de DeltaV gasté el motor más eficiente que hay en KSP, y el único que es una concesión a la "tecnología futura". El LV-N es un motor nuclear térmico que está basado en el motor real NERVA desarrollado por la NASA.

En el juego, el LV-N tiene el Isp en el vacío más alto de todos los motores, 800s. Para compensar, el empuje es irrisorio comparado con los motores químicos del juego: escasos 60kN. En la realidad, el motor NERVA tenía un Isp de 850s y 336 kN de empuje, pero en el juego redujeron el empuje para que no fuera excesivamente mejor que los motores químicos, de modo que no tuviera sentido gastar otro motor que el LV-N.

El LV-N es, además, uno de los motores más pesados, con 3 toneladas.

Todo esto significa que para conseguir una DeltaV elevada con este motor tenemos que tener en cuenta que vamos a tener un empuje muy pequeño, y en ese caso o nos resignamos a tener encendidos muy largos, o ponemos más motores, elevando el peso seco de la nave y reduciendo así la DeltaV. En resumidas cuentas, el LV-N está indicado para naves muy grandes que lleven mucho propelente para compensar el peso del motor.

Hay otro problema que quizá sea anecdótico, pero que me gustaría mencionar. El tanque naranja que se ve en la imagen era el tanque más grande que había en el momento que construí la nave. Por aquel entonces, el LV-N no estaba correctamente implementado y consumía oxidante y combustible como si fuera un motor químico. Esto lo cambiaron en las últimas versiones, y el LV-N consume ahora sólo combustible (hidrógeno líquido), como el motor real. Pero el tanque no lo cambiaron... de forma que si el tanque está lleno, el oxidante es peso muerto (porque el motor no lo consume), y si quito el oxidante, llevo el tanque medio lleno, lo cual significa que la relación entre masa total y masa de propelente en el tanque es bastante mala y afecta a la DeltaV.

Como se puede ver en la imagen, este módulo de propulsión tiene una DeltaV de 5105 m/s sin carga. La DeltaV disminuirá en cuanto le añada otros módulos.

Después de varias iteraciones de diseño, mi siguiente idea de un módulo de propulsión fue esta, con el también ocurrente nombre de Orbital Ferry MkVI:

(Aquí es donde salta mi instinto de programador, y desearía que hubiera un sistema de versionado como CSV en KSP para archivar las versiones de las naves que uno monta y prueba de forma iterativa).

El diseño básico es el mismo, cuatro motores LV-N con un cuerpo central. La diferencia es que para ese cuerpo central he gastado un fuselaje de avión que, como he comentado más arriba, sólo contiene combustible, y ya no se desperdicia capacidad con el oxidante. Como tenía más espacio, añadí dos puertos de atraque pequeños a los lados.

El rectángulo blanco grande en el centro del fuselaje es un radiador extensible. En las últimas versiones de KSP se implementó el modelado del flujo de calor en las naves. Principalmente, ciertos componentes producen calor (los motores y los taladros de extracción), y hay que gestionar la eliminación del calor o los componentes se recalientan y explotan.

También está modelado el flujo de calor en la reentrada, pero ahí hay que hacer uso de escudos térmicos. Al menos, no sé de nadie que haya diseñado una cápsula de reentrada que disipe con un radiadorcito los miles de grados en que se calienta una cápsula al entrar en una atmósfera a varios kilómetros por segundo.

El motivo por el que añadí el radiador por si acaso es que los LV-N generan mucho calor, y hace varias versiones tendían a explotar en encendidos largos (que es casi todos los encendidos, dado el empuje tan bajo que tienen).

Este módulo de propulsión tiene 7213m/s de DeltaV sin carga, y tiene más posibilidades de ampliación.

A continuación me gustaría mostrar el módulo de control y habitáculo:

El módulo de mando delantero tiene una capacidad de tres tripulantes, y el módulo cilíndrico justo detrás tiene una capacidad de cuatro tripulantes. Aquí en donde hago un poco de "roleplay": en la misión sólo voy a tener tres kerbals en total, para simular una misión real en la que los tripulantes necesitan algo de espacio personal. En principio podría meter siete kerbals - los kerbals no se quejan aunque tengan que pasar años sentados en la cabina como si fueran en una lata de sardinas. De hecho, me podría ahorrar el módulo de control y habitáculo y acoplar el módulo de aterrizaje directamente al módulo de propulsión, lo cual me ahorraría bastante DeltaV. Pero, en fin, uno vive para plantearse desafíos...

Y para terminar, este es mi módulo de aterrizaje para Duna:

Está basado en el módulo de aterrizaje que usaba para los vuelos a Mun, y para la misión a Duna añadí paracaídas y un escudo térmico.

El módulo tiene una tripulación de dos kerbals, y una DeltaV de 2245 m/s, que debería ser suficiente para aterrizar y volver a despegar de Duna. Como Duna tiene una atmósfera, aunque muy tenue, espero poder utilizarla para frenar la cápsula y ahorrar algo de DeltaV.

Vale la pena mencionar que los cuato motores cohete pequeños del módulo tienen el mismo empuje que los cuatro LV-N del módulo de propulsión, 240 kN.

Hay un par de cosas que tengo que mencionar. Aparentemente, según he leído en los foros, la atmósfera de Duna es tan poco densa que no sería necesario el escudo térmico. Los tests del módulo los hice en Kerbin, donde el escudo térmico es absolutamente imprescindible.

Y los tests me llevaron bastante tiempo (así junta uno 300 horas en el juego), porque tuve que iterar el diseño varias veces. El módulo tiene dos juegos de paracaídas: cuatro paracaídas "drogue" (que creo que se traduce al castellano como paracaídas piloto), que se abren a mayor altitud, tienen más tolerancia a las altas velocidades, y empiezan el frenado de la cápsula. Hay además otros cuatro paracaídas principales, que se abren a menor altitud y frenan la cápsula hasta que acaba en una velocidad aceptable para el aterrizaje (como máximo, unos 10 m/s de velocidad vertical es aceptable).

Sin los paracaídas piloto, en la atmósfera de Kerbin hay una ventana muy pequeña entre el momento en el que la velocidad es demasiado alta como para abrir los paracaídas principales (en ese caso, los paracaídas se rompen directamente), y el momento en el que la atmósfera es suficientemente densa como para que los paracaídas se abran correctamente. En ese caso, el frenazo los arranca de la cápsula, junto con cualquier elemento estructural al cual estuvieran sujetos. Uno se encuentra, pues, con una cápsula medio rota, a algunos centenares de metros sobre el suelo, y en caída libre. Lo cual significa que para la tripulación de la cápsula, el resto de su vida va a ser muy excitante y muy corto.

En cualquier caso, después de un concienzudo programa de test, la cápsula funciona correctamente en Kerbin... pero no tengo ni idea de si va a funcionar en Duna. Mi única experiencia es una sonda que conseguí aterrizar en Duna, y me sorprendió lo poco que dura el frenado atmosférico, y lo poco que frena la atmósfera, de forma que el final del proceso de aterrizaje se tiene que hacer con cohetes. Igual que en Marte, de hecho.

Me voy a detener aquí. En el próximo post mostraré qué aspecto tienen las naves una vez ensambladas en órbita, y como se programan en el juego las maniobras orbitales para el viaje interplanetario.

Vámonos a Duna - Parte I: Un poco de astrodinámica

Kerbal Space Program es un juego / simulador de vuelo espacial que se ha hecho legendario en Internet. Han habido pocos juegos que hayan incluído vuelo espacial realista, porque el vuelo espacial es muy complejo como para ser divertido (aparte de unos cuantos pillados entre los que me incluyo), y porque el vuelo espacial real es muy diferente de como estamos acostumbrados a verlo en las películas.

El mérito de Kerbal Space Program es que incluye un modelo físico realista aunque simplificado (incluyendo gravedad y efectos atmosféricos), de forma que es relativamente accesible, pero suficientemente riguroso como para que uno acabe aprendiendo astrodinámica real.

Como no podía fallar, hay un cómic de xkcd al respecto.

Advierto: jugar a menudo al KSP arruina la experiencia de ver películas de ciencia ficción. Por otro lado, hace mucho más fácil seguir eventos científicos como el vuelo de la sonda Rosetta, New Horizons o Juno.

Trasteando con KSP uno aprende cosas como diseñar un cohete multietapa para entra en órbita, hacer citas orbitales, atracar, enviar sondas a la luna o planear una expedición interplanetaria. Que es lo que nos ocupa.

Parte de la accesibilidad de KSP es que uno diseña cohetes a base de ensamblar piezas estándar (un poco como jugar con lego) para luego poner una capsula tripulada en órbita... o provocar enormes explosiones. Lo que hace KSP a la vez entrañable y poco serio es que uno no trabaja con astronautas humanos, sino con "Kerbals", una especie de humanoides verdes con un profundo amor por la ingeniería y a su vez poco respeto por su propia integridad física.

El planeta donde viven los Kerbals se llama Kerbin, y tiene dos lunas, Mun y Minmus. El sol se llama Kerbol, y el resto del sistema solar está basado en nuestro sistema solar.

El planeta más cercano a Kerbol es Moho, basado en Mercurio. El siguiente planeta es Eve, que tiene una atmósfera muy densa y es el equivalente de Venus.
(Enviar una expedición tripulada de ida y vuelta a Eve es uno de los desafíos más grandes que uno pueda plantearse en KSP).

Después de Kerbin viene Duna, un planeta rojo con casquetes polares que es el equivalente de Marte. El siguiente cuerpo celeste por orden de lejanía es el planetoide Dres, el equivalente de Ceres.
Tras Ceres viene Jool, el equivalente de Júpiter, y al igual que en nuestro sistema solar, el planeta más interesante, con cinco satélites: Laythe, Vall, Tylo, Bop y Pol. Laythe es especialmente interesante, porque es un satélite oceanico con varios archipiélagos dispersos en su superficie, y una atmósfera no respirable pero similar a la de Kerbin, de forma que el cielo es azul y ofrece tremendas vistas de Jool, dado que es el satélite más cercano.

El último planeta es Eelo, el equivalente de Plutón, aunque por aspecto se parece más a la luna Europa de Júpiter.

Tengo KSP desde hace unos años, y es el juego de Steam en el que tengo más horas invertidas (unas 300, más o menos). Pero hasta ahora no había ido más lejos que hacer misiones a las lunas de Kerbin, y enviar sondas no tripuladas a Eve y Duna. Así es que he estado implementando mi primera misión tripulada a Duna.

Antes de explicar el proceso de planificación, tengo que decir que uno de los motivos por los que KSP se ha hecho tan popular es que es un juego muy abierto a la modificación, de forma que hay centenares de "mods" que convierten KSP de un juego curioso en un excelente simulador espacial. Yo mismo tengo una docena de mods instalados. Parte de ellos son mods gráficos, que añaden nubes y efectos de dispersión atmosférica, y parte de ellos son herramientas sin las cuales sería dificilísimo hacer nada serio en KSP.

Tengo que mencionar que hay un "cisma" importante entre los usuarios de KSP. Unos dicen que la mejor forma de jugar es hacerlo todo a ojo y sin preocuparse de la precisión técnica, y son la gente que denigra los mods que añaden herramientas.

Otros, entre los que me incluyo, queremos usar KSP para intentar implementar misiones "realistas", de forma que es imprescindible tener instrumentos que ayuden en la navegación del espacio.
La navegación espacial real no es en absoluto intuitiva, y las naves espaciales reales tienen multitud de instrumentos (y apoyo desde la Tierra) para saber en todo momento dónde están, en qué dirección se mueven, y cómo realizar maniobras.

Es cierto que para viajar de Kerbin a sus lunas se puede volar a ojo. Pero yendo a ojo es imposible realizar expediciones interplanetarias.

Dicho esto, pongámonos manos a la obra.

Hay dos magnitudes importantísimas a la hora de diseñar un cohete: DeltaV y TWR, o Thrust-to-Weight Ratio.

TWR es la magnitud más fácil de explicar: es la relación entre el peso del cohete o nave espacial y el empuje (en unidades de fuerza) de los motores. Para un cohete que tenga que despegar de una superficie planetaria, hace falta una TWR de entre 1.5 a 2. Menos de esto, y el cohete no se levantará de la plataforma de despegue. Más de esto, y el cohete estará empujando contra la atmósfera y desperdiciando propelente.

Para naves que sólo vayan a usarse en órbita (o sea, sin aterrzar), el TWR no es muy importante, y sólo influye en la duración de los encendidos. Cuanto más bajo sea el TWR, menor sera la aceleración, y más durarán los encendidos durante las maniobras.

Así es que, en un cohete multietapas, la etapa inferior la diseñaremos de forma que tengamos una TWR alta, mientras que las etapas superiores, o el vehículo que lleva la carga de pago, sólo van a necesitar una TWR baja.

Pero podemos usar motores que nos den una TWR alta para hacer maniobras más rápidamente. Por ejemplo, para entrar en una órbita de transferencia entre Kerbin y Mun, con una TWR baja puede que haga falta encender los motores un par de minutos, mientras que con una TWR alta puede que sólo nos hagan falta 30 segundos.

Y ahora hablemos de la DeltaV, que es el pan nuestro de cada día de todos los Kerbonautas.

DeltaV es la cantidad de cambio de velocidad que tiene un vehículo, dependiendo de la masa total del vehículo, la masa de propelente y la eficiencia del motor. El uso de DeltaV es muy práctico, porque nos permite saber qué maniobras son posibles con el propelente que tenemos en el vehículo. Si digo que me quedan dos toneladas de propelente en el vehículo, no tendré ni idea de que puedo hacer con él. Pero si digo que me queda una DeltaV de 1000 m/s, y yo se que para ir a Mun desde una órbita baja en Kerbin necesito una DeltaV de unos 800 m/s, sabré que tengo suficiente propelente para hacer la maniobra.
Una pequeña aclaración: cuando estoy hablando de DeltaV para ir de una órbita a otra, estoy mencionando sólo la magnitud del cambio de velocidad, y no la dirección. A efectos de calcular el presupuesto energético del que dispongo, es suficiente con hablar de DeltaV como una magnitud escalar. La orientación del vehículo cuando cambie de una órbita a otra no es relevante para esta discusión, pero la mencionaré si es necesario.

La DeltaV proviene de la ecuación del cohete de Tsiolkovsky. En ella se asume que un cohete se mueve en una dirección a partir de la expulsión de material (propelente) en la dirección contraria, tal y como lo permite la tercera ley de Newton. La ecuación del cohete vale siempre que estemos hablando de cohetes que carguen su propio propelente, ya sean motores químicos, nucleares, o de antimateria.

Me voy a permitir poner aquí la ecuación de la DeltaV, porque es importante tenerla a la vista para nuestros propósitos:
 

En esta formulación de la ecuación del cohete, tenemos Vexh, que es la velocidad a la que se expulsa el propelente, la fracción de masas m0/m1, que es la relación entre la masa total del vehículo y la masa "seca" del vehículo (o sea, sin propelente).

Se puede apreciar que para conseguir más DeltaV tenemos que hacer que el vehículo contenga tanto propelente como sea posible, y dado que la carga de pago es generalmente fija, queremos que el resto de masa del vehículo (habitualmente, masa estructural) sea lo más pequeña posible. En cohetes reales no es raro que la fracción de masa sea 0.8 o mayor.

Para propósitos de planificación, es ventajoso expresar Vexh (o Ve) como:

Donde g0 es la aceleración de la gravedad en la superficie de la tierra, e Isp es el impulso específico, que es una cantidad algo rara y poco intuitiva pero que nos permite comparar motores entre sí.

Isp es el impulso específico de un motor cohete, y tiene unas unidades algo raras (segundos), pero nos da una idea de la eficiencia de un motor cohete. Isp es el empuje que nos proporciona un motor por unidad de peso de propelente que fluye por él. O sea, cuánto empuje generamos por unidad de propelente expelida.

Dado que el empuje tiene unidades de fuerza, y el peso también, nos queda que empuje / (peso/segundo) nos da unidades de segundos. Esta es la formulación más habitual del Isp.
Hay que tener en cuenta que la eficiencia de un motor cohete depende de la presión ambiental, y por ello, el Isp varía según estemos al nivel del mar o en el vacío. El Isp en el vacío es mayor que al nivel del mar.

Lo importante es que para conseguir una mayor DeltaV nos conviene que el impulso específico sea lo más grande posible. Para hacerse una idea, los motores principales del Space Shuttle (SSME) tenían un Isp de 453s, los motores F1 de la primera etapa del Saturn V tenían un Isp de 265s al nivelo del mar y 304s en el vacío, y los motores J2 de las etapas superiores del Saturn V tenían un Isp de 424s en el vacío.

Los motores en KSP tienen Isp alrededor de estos valores, de forma que los cohetes que uno diseña tienen capacidades más o menos realistas: uno tiene que utilizar técnicas reales para realizar viajes espaciales, y no es posible salir zumbando de un lado al otro del sistema solar con un chorrito de combustible. Esto no es Star Wars, chicos.

Todo esto que he contado vale para un vehículo de una sola etapa. Ahora bien, una forma de mejorar la fracción de masa de un cohete es dividirlo en varias etapas, de forma que nos vayamos deshaciendo del peso muerto de masa estructural y motores según vayamos expulsando el propelente. Diseñar un vehículo de múltiples etapas es un problema de optimización bastante complejo, así es que la forma apróximada de calcular la DeltaV de todo el vehículo es calcular la DeltaV de cada etapa, para lo cual asumimos que todas las etapas que estan por encima de la que estamos calculando son peso muerto, y al final sumamos la DeltaV de todas las etapas. En la página de Project Rho hay un tratado algo más extenso sobre el diseño de un cohete de varias etapas.

Aquí vuelvo al tema de los mods en KSP que he comentado arriba: el juego en sí no permite calcular la DeltaV de un cohete cuando lo estamos construyendo, pero hay herramientas que nos calculan la DeltaV de cada etapa del cohete, lo cual nos permite planificar cómo queremos distribuir la DeltaV.

Por ejemplo, supongamos que queremos enviar un pequeño módulo de aterrizaje tripulado para ir a Mun y volver. Podemos diseñarlo así:

• La primera etapa nos da la DeltaV para despegar y poner el cohete en órbita.
• La segunda etapa nos da la DeltaV para ir a Mun, entrar en órbita, y si queda algo de margen, ejecutar parte o toda la maniobra de aterrizaje.
• El módulo tripulado nos da la DeltaV para aterrizar en Mun, volver a despegar y salir de la órbita de Mun, de forma que la trayectoria entre en la atmósfera de Kerbin.
• La cabina del módulo tripulado la separamos del resto, y le ponemos un escudo térmico y paracaidas, de forma que una vez la trayectoria orbital entre en la atmósfera, el rozamiento nos frene y podamos hacer un aterrizaje suave, sin necesitar más propelente.

Para planificar las misiones, los usuarios de KSP han hecho mapas de DeltaV, parecidos a los mapas del metro, que listan la DeltaV para ir a diferentes partes del sistema kerbolar, partiendo de Kerbin:

Para hacer este mapa se han asumido varias cosas. Principalmente, se supone que para ir de un cuerpo a otro, uno utiliza la trayectoria óptima en términos de consumo de fuel, esto es, una órbita de transferencia de Hohmann. De las órbitas de transferencia de Hohmann hablaré más abajo.


Esto no tiene que ser siempre el caso, pero lo único que hay que tener en cuenta es que, si no uso una transferencia de Hohmann, voy a necesitar más DeltaV. Este mapa, pues, me da el gasto mínimo de DeltaV que necesito para ir de un sitio a otro, y generalmente tendré que planear mi vehículo con algo de margen.


Por ejemplo, supongamos que quiero ir de Kerbin a Mun. Necesitaré 3400m/s para despegar y entrar en una órbita baja, 860m/s para entrar en una órbita de transferencia a Mun, 360m/s para entrar en órbita en Mun, y 580m/s para aterrizar. O sea, que mi cohete deberá tener al menos 5200m/s de DeltaV en el momento del lanzamiento. Si además quiero volver, tendré que dieseñar mi vehículo con aún más DeltaV.


Para poner una sonda en la superficie de Duna, necesito un cohete con unos 6540m/s de DeltaV. Para una carga de pago pequeña, esto no es un cohete necesariamente muy grande. Si quiero llevar una nave tripulada, y quiero volver, necesito otros 3140m/s de DeltaV.

Si quiero llevar una cabina de mando y un módulo de habitáculo, el cohete empieza a ser gigantesco, así es que puede ser ventajoso montar el vehículo en órbita (requiriendo varios lanzamientos). Además, en estos casos conviene separar el vehículo de transferencia (que incluirá los motores, tanques de propelente y el habitáculo de la tripulación),del módulo de aterrizaje, de forma que para aterrizar no necesitamos tanto propelente (porque no aterriza toda la nave), y a la vuelta desechamos el módulo de aterrizaje, de forma que ahorramos propelente no teniendo que cargar con él.
(Esto es lo que hicieron las misiones Apollo).


Quiero terminar este largo post hablando de cómo se planea un viaje entre planetas. Si quiero usar una órbita de transferencia de Hohmann, tengo que esperar a que los planetas estén alineados para que, empezando el viaje en un momento determinado, el planeta de destino esté en el punto de su órbita en el que intercepta a mi órbita de transferencia.


Volvamos a las órbitas de Hohmann. Una transferencia de Hohmann es una órbita elíptica que se utiliza para pasar de una órbita a otra alrededor de un cuerpo central (vamos a asumir que tanto la órbita de origen como la de destino son circulares). La órbita de transferencia tiene la periapsis en la órbita más baja, y la apoapsis en la órbita más alta. Supongamos que queremos pasar de la órbita más baja a la órbita más alta. Para entrar en la órbita de transferencia, efectuaríamos un encendido en la dirección del movimiento (lo cual se llama progrado) cuando nuestra órbita y la de transferencia se tocan. Posteriormente, una vez lleguemos al punto donde la órbita de transferencia y la órbita superior se tocan, volveríamos a efectuar un encendido en la dirección del movimiento para circularizar nuestra órbita.
Para pasar de una órbita más alta a una más baja, el procedimiento es el mismo, realizando los encendidos contra la dirección del movimiento (retrógrado).

By Leafnode - Own work based on image by Hubert Bartkowiak, CC BY-SA 2.5, Link

Para este tipo de maniobra se asume que los encendidos suceden idealmente en un tiempo infinitesimalmente pequeño. En un motor real tenemos que encender el motor durante un tiempo determinado (no nulo) para efectuar el cambio de velocidad que necesitamos, perdiendo un poco de eficiencia.


El problema lo podemos plantear así: si uso una órbita de transferencia con un tiempo de vuelo conocido, quiero saber en qué punto de la órbita del planeta de origen tengo que iniciar el viaje para encontrarme el planeta de destino en el punto en el que mi órbita de transferencia y la del planeta de destino se encuientran.


El ángulo entre los vectores de los planetas de origen y destino al iniciar el viaje se llama phasing angle (ángulo de fase). En esta página está explicado como calcularlo, pero los usuarios de KSP son muy listos y han creado un applet para calcularlo automáticamente sin tener que ocuparse de las matemáticas.


Este punto de la órbita en el que tenemos que iniciar el viaje para poder usar una órbita de transferencia de Hohmann es lo que se denomina transfer window (ventana de transferencia). Como queremos ahorrar energía (o sea, utilizar la menor DeltaV posible), no podemos enviar misiones a Marte (o en KSP, a Duna) cuando nos de la gana, sino cuando los planetas estén alineados adecuadamente.


Hay una forma todavía más sofisticada de encontrar el momento correcto para iniciar una transferencia interplanetaria. Es lo que se denomina porkchop plot, o algo así como "diagrama de costillas de cerdo". Este es el método que utiliza la NASA para planificar sus misiones.

Lo que es el porkchop plot está explicado aquí o aquí. El porkchop plot es una representación gráfica de las soluciones del problema de Lambert. El problema de Lambert consiste en encontrar una órbita que pase por dos puntos en el espacio y tenga un tiempo de tránsito determinado. Este problema se puede resolver analíticamente, o utilizando métodos iterativos. Representando gráficamente las soluciones del problema de Lambert obtenemos el porkchop plot: en este diagrama, los ejes representan el tiempo de partida y el tiempo de llegada para una transferencia entre dos cuerpos celestes, y la tercera coordenada es la energía característica de la órbita que resuelve el problema. Las curvas de nivel, pues, son curvas que unen las soluciones de igual energía. Para encontrar la órbita de menor consumo de energía (menor DeltaV), buscaremos los valles del porkchop plot.

El porkchop plot puede representarse con curvas de nivel, como en el artículo de Wikipedia, pero también se puede representar con colores, como han hecho aquí. Sin siquiera entender las matemáticas, puedo introducir el planeta de origen y el de destino, y en el porkchop plot tengo representada la DeltaV que necesito para una fecha de salida y un tiempo de tránsito determinados. La DeltaV está representada en colores, y el azul oscuro representa el mínimo de DeltaV. Así es que pulsando en el diagrama en un punto determinado, dependiendo de cuánta DeltaV quiera consumir, los ejes me dicen cuándo tengo que iniciar el viaje interplanetario y cuánto durará el viaje.


En una misión real tripulada, el tiempo de viaje es vital a la hora de saber qué cantidad de suministros necesito para tener a la tripulación viva y en condiciones de trabajar. El consumo de alimentos y oxígeno no está incluído en el KSP básico... pero hay mods que lo añaden, para aumentar el realismo y tener un desafío más al que enfrentarse.


Hasta aquí llega la teoría de la planificación de misiones interplanetarias. En el próximo post explicaré qué preparativos he hecho para enviar kerbals a Duna.